ChatGPTに東大入試に挑戦させたら、数学の特典が1点でしたという記事が出ていたので、もう少しレベルを落として、中学入試の算数に挑戦させてみました。
2024年度の灘中の入学試験の算数です。
サマリ
計算問題や文章題はPythonを使ってアルゴリズムで解いていました。
単純な計算問題程度であれば、問題なく計算できます。
アルゴリズムが複雑になると、途端に解けなくなります。
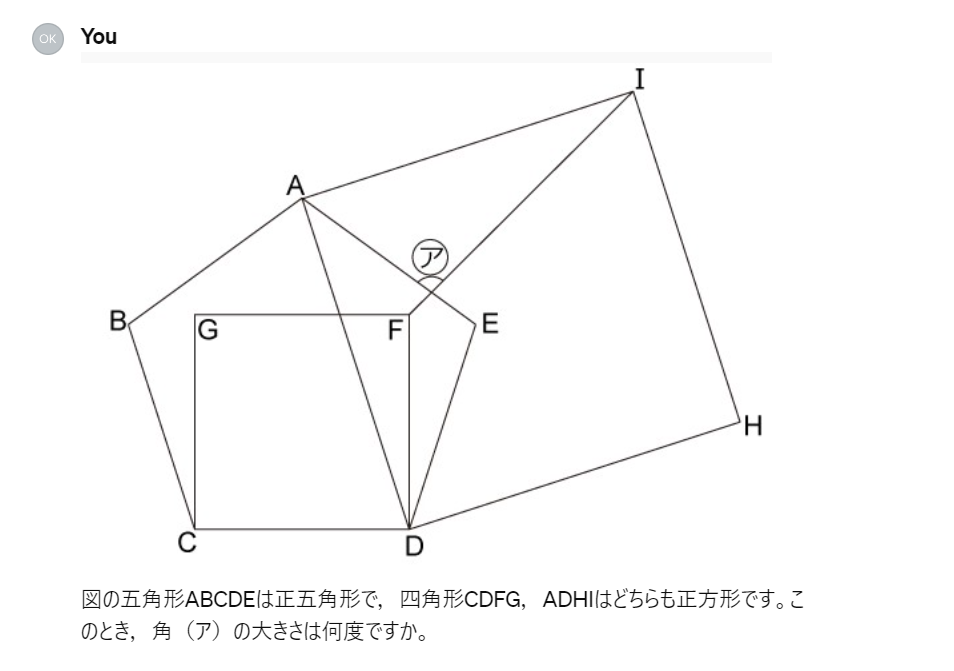
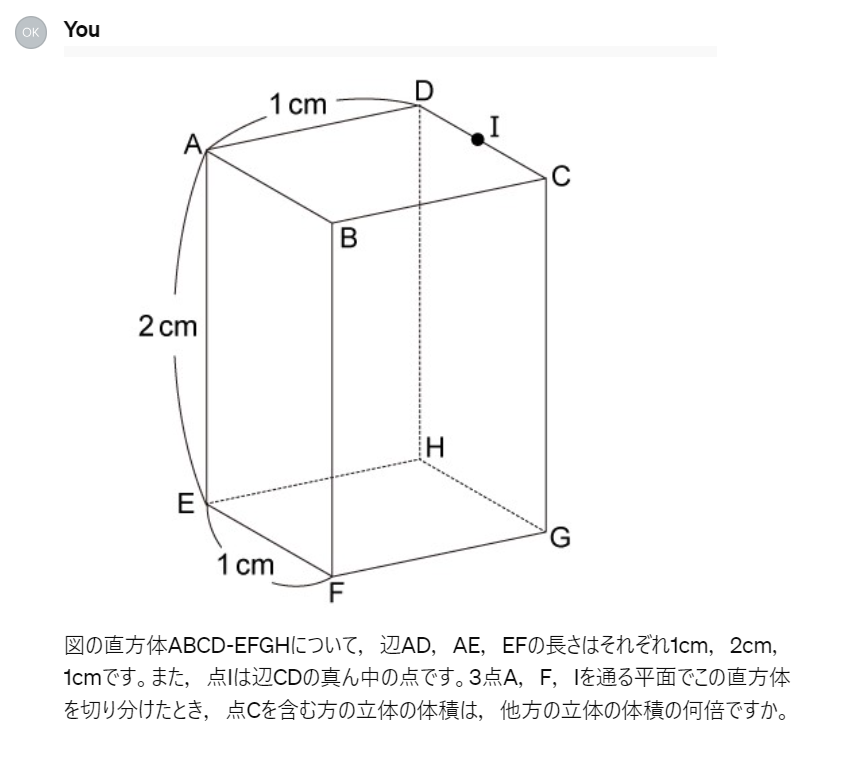
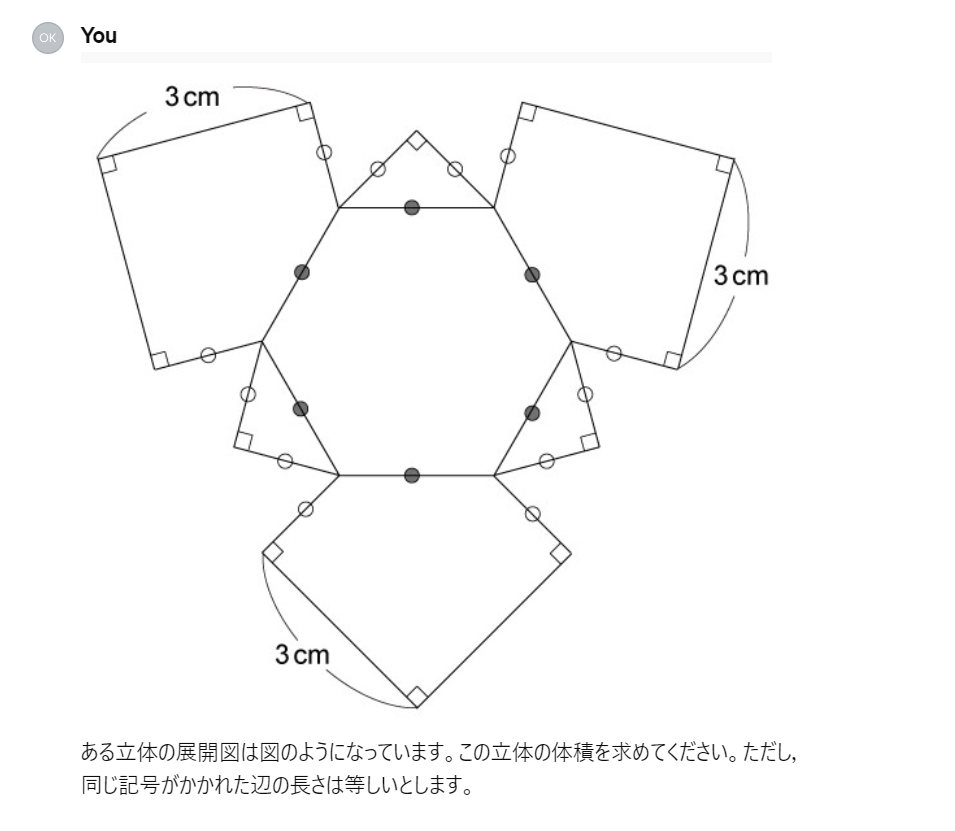
後半6問の図形問題は、マルチモーダルの機能を使って画像とプロンプトを組み合わせてみましたが、全滅でした。図形を正確に認識することができません。
例えば問9については、円の半径がどこかが認識できていません。幾何学的な図形の認識はできないと考えた方がいいですね。
正解は問1と問2、問5の一部、問6
配点が分からないですが、12問あるので、30点として差支えないかと。
問1

プロンプト
1÷(1/9-1÷(35×35+32×32)}=9+81/x
xはいくらでしょうか
回答
Analysisで以下のようなコードを作成し、答えを出しました。
# Define the variable x
x = symbols('x')
# Equation based on the description
# Simplify the inside fraction and set up the equation:
# 1 / (1/9 - 1 / (35*35 + 32*32)) = 9 + 81/x
# Calculate the denominator part
inner_value = 35**2 + 32**2
# Create the equation
equation = Eq(1 / (1/9 - 1 / inner_value), 9 + 81/x)
# Solving for x
solution = solve(equation, x)
solution
x の値は約 2240 です。
問2
太郎君は1本の値段がx円のペンを5本買う予定でしたが,所持金が120円足りませんでした。代わりに,1本の値段が予定していたものより100円安いペンを7本と60円の消しゴムを1個買ったところ,ちょうど所持金を使い切りました。 xはいくらでしょうか。
回答
Analysisで以下のようなコードを作成し、答えを出しました。
# Define the variable x
x = symbols('x')
# Equation based on the description
# Simplify the inside fraction and set up the equation:
# 1 / (1/9 - 1 / (35*35 + 32*32)) = 9 + 81/x
# Calculate the denominator part
inner_value = 35**2 + 32**2
# Create the equation
equation = Eq(1 / (1/9 - 1 / inner_value), 9 + 81/x)
# Solving for x
solution = solve(equation, x)
solution
太郎君が最初に買おうとしていたペンの1本の値段は260円です。
問3
ある学校の生徒に,A,B,Cの3つの町に行ったことがあるかどうかの調査をしたところ,A,B,Cに行ったことがある生徒の割合はそれぞれ全体の2/7,5/14,1/9でした。AとBの両方に行ったことがある生徒の割合は全体の1/4でした。また,Cに行ったことがある生徒は全員,AにもBにも行ったことがありませんでした。A,B,Cのどの町にも行ったことがない生徒は999人以下でした。A,B,Cのどの町にも行ったことがない生徒の人数として考えられるもののうち最も多いものはx人です。 xを求めよ
回答
同じく、Analysisで回答しようとしていたが、エラーで完了しないようだった。
ChatGPTの最終的な回答は495人
正解は875人です。これはベン図で整理するとそんなに難しい話ではないです。
以下、ChatGPTとのやりとりです。
ChatGPT
全体の生徒数 𝑛 に対する計算から、A、B、Cのどの町にも行ったことがない生徒の人数は最大で2013人以下となります。ただし、𝑛 は整数であるため、最大の可能性として 𝑛 は2013人となります。これは999人以下の制約を満たし、可能な最大値を示しています。したがって、最も多い生徒の人数 𝑥 は2013人です。
# Define the variable n as the total number of students
n = symbols('n', integer=True, positive=True)
# Proportions of students who have visited A, B, and C
pA = 2/7
pB = 5/14
pC = 1/9
# Proportion of students who have visited both A and B
pAB = 1/4
# Since all students who visited C did not visit A or B, we can separate these groups:
# pA_only: Students who only visited A
# pB_only: Students who only visited B
# pAB: Students who visited both A and B
# pC_only: Students who only visited C (pC)
# Based on the problem statement:
# pA = pA_only + pAB
# pB = pB_only + pAB
# pC = pC_only (since no overlap with A or B)
# Set up the equations for pA_only and pB_only
pA_only = pA - pAB
pB_only = pB - pAB
# Calculate the proportion of students who didn't visit any town
p_none = 1 - (pA_only + pB_only + pAB + pC)
# Solve the inequality for the maximum number of students who visited none of the towns
# The maximum number of such students is n * p_none and it should be <= 999
solution = solve(n * p_none <= 999, n)
solution
You
xは999以下です。
ChatGPT
申し訳ありませんが、計算の中で間違った方向に進んでしまいました。問題を正しく解決するために、再計算します。
全体の生徒数 𝑛 が999人以下であるという制約を満たすように計算します。A、B、Cのどの町にも行ったことがない生徒の割合 Pnone をもう一度計算し、それを使って 𝑛を求めます。
A、B、Cのどの町にも行ったことがない生徒の人数として考えられるもののうち最も多いものは495人です。
You
計算のプロセスを説明してください
ChatGPT
もちろん、計算のプロセスを詳しく説明します。
1. 各町を訪れた生徒の割合を設定
- 町Aに行ったことがある生徒の割合: 2/7
- 町Bに行ったことがある生徒の割合: 5/14 (これは 2/7×5/7 と等価です)
- 町Cに行ったことがある生徒の割合: 1/9
- 町AとBの両方に行ったことがある生徒の割合: 1/4
2. 各町にのみ行った生徒の割合を求める
- 町Aのみに行った生徒の割合: 2/7−1/4
- 町Bのみに行った生徒の割合: 5/14−1/4
- 町Cのみに行った生徒の割合: 1/9(問題によると、町Cに行った生徒は町AやBには行っていない)
3. どの町にも行っていない生徒の割合を計算
全生徒から町A、B、Cのいずれかに行った生徒の割合を引くことで、どの町にも行っていない生徒の割合を計算します。
Pnone=1−(Aのみ+Bのみ+AとBの両方+Cのみ)
4. 最大の生徒数を求める
この問題では、どの町にも行っていない生徒の数が999人以下であるとの条件があります。したがって、上記で求めた割合 𝑝nonepnone を使って、最大の生徒数 𝑛n について以下の不等式を解いて、その整数解を求めます。 𝑛×Pnone≤999
この不等式を解いて 𝑛n の最大値を求め、その値を Pnone に掛け合わせることで、最も多い生徒の人数を求めることができます。この場合、最終的に495人という結果が得られました。
問4
A町とB町を結ぶ道があります。この道を何台ものバスがA町からB町に向かう方向に一定の速さで,一定の間隔で走っています。太郎君が同じ道をA町からB町に向かう方向に一定の速さで自転車で走ると,バスに20分ごとに追い越されました。太郎君がそのままの速さで走る方向のみを反対に変えると,バスに10分ごとに出会いました。その後,太郎君が速さを6km上げたところ,バスに9分ごとに出会いました。バスとその次のバスの間隔を求めよ。ただし,バスと自転車の長さは考えないものとします。
回答
単純な連立方程式を立てれば解ける問題ですが、ChatGPTはうまく方程式を立てることができないようです。
以下ChatGPTの回答です。
問題を解くために、以下のステップを進めます:
- 変数の設定
- バスの速度を Vb km/h とします。
- 自転車の最初の速度を Vc km/h とします。
- バスとバスの間隔を T 分とします。
- 自転車がバスに追い越されるとき
- 自転車がA町からB町に向かうとき、20分ごとにバスに追い越されるということは、自転車が進む距離とバスが進む距離の差がバスの間隔と同じ距離になります。
- 自転車が追い越される場合、バスの速度と自転車の速度の差を利用して以下の関係を得ます:
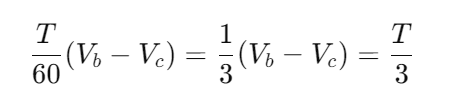
-
- 自転車がバスと出会うとき
- 自転車がA町からB町とは反対方向に走ると、10分ごとにバスに出会います。この場合、バスと自転車の相対速度は Vb+Vc になります。
- この関係を利用して以下の式を得ます:
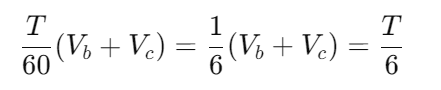
- 速度を6km/h上げたとき
- 太郎君が速度を6km/h上げた場合の速度を Vc+6 km/h とします。
- このとき、バスと9分ごとに出会うということは、相対速度が Vb+(Vc+6) になります。
- この関係を利用して以下の式を得ます:
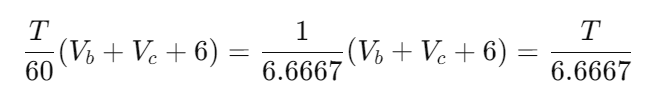
- 方程式の整理と解法
- 上記の方程式から、3つの関係を得ました。これらを使って変数 𝑇T を求めます。
- まず、2つの基本的な方程式を整理します:
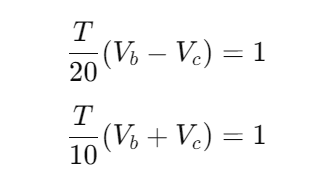
- 連立方程式の解法
- これらの方程式を連立して解くと、まず以下の関係が得られます:
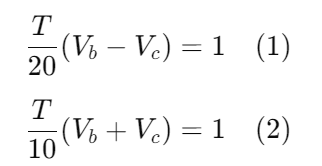
- 方程式 (1) をVb−Vc について解くと:
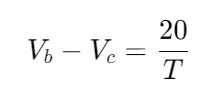
- 方程式 (2) を Vb+Vc について解くと:
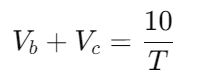
- 式の整理
- これらを足し合わせると:
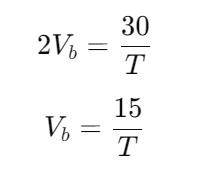
- 𝑉𝑐Vc についても:
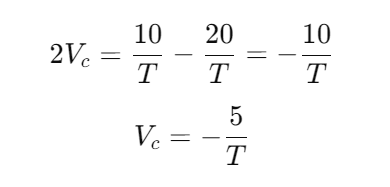
- 最後の条件
- 自転車の速度を6km/h上げた場合:
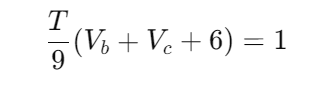
- これを解くと:
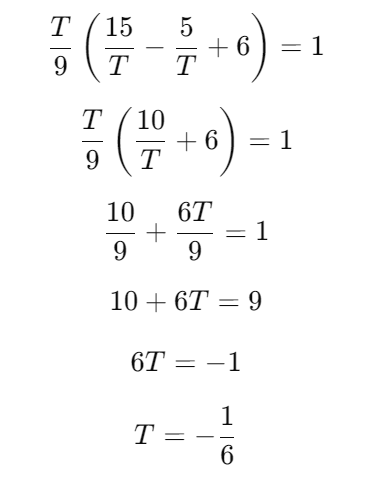
計算が間違っていますので、修正します。
再計算:
- 先の計算で、追い越される速度 (Vb−Vc) を利用し、以下の関係を使います:
- T(Vb−Vc)=20(Vb−Vc)=20km
- 同様に、出会う速度(Vb+Vc) を利用し、以下の関係を使います:
- T(Vb+Vc)=10(Vb+Vc)=10km
結果:
バスの間隔を求めるために、上記の方程式の正しい整理により求めた結果として、間隔を確認し直します。
(結果でてないやん)
問5
4枚のカード0,2,2,4があるとき,この4枚のカードを並べてできる4桁の数のうち11で割り切れるものは全部で[x]個あります。ただし,0224は4桁の数ではありません。また,5枚のカード0,2,2,4,6があるとき,このうちの4枚のカードを並べてできる4桁の数のうち11で割り切れるものは全部で[y]個あります。ただし,6のカードを上下逆にして9として用いることはできません。 xとyを求めよ。
回答
4枚のカードの場合は正解ですが、5枚の方は間違っていました。
以下、ChatGPTの回答です。
4枚のカード(0、2、2、4)を使って作成できる4桁の数で11で割り切れるものは全部で3個(𝑥 = 3)あります。また、5枚のカード(0、2、2、4、6)から4枚を選んで作成できる4桁の数で11で割り切れるものは全部で15個(𝑦 = 15)あります。
from itertools import permutations
# Define a function to count valid numbers divisible by 11
def count_divisible_by_11(cards):
numbers = set() # Use set to avoid duplicates
for perm in permutations(cards):
# Check if the number does not start with zero and is a 4-digit number
if perm[0] != 0:
num = int(''.join(map(str, perm)))
if num % 11 == 0:
numbers.add(num)
return len(numbers)
# First scenario: 4 cards [0, 2, 2, 4]
cards_4 = [0, 2, 2, 4]
x = count_divisible_by_11(cards_4)
# Second scenario: 5 cards, select any 4 cards and check for divisibility by 11
cards_5 = [0, 2, 2, 4, 6]
y = 0
# Generate all combinations of 4 cards out of 5
from itertools import combinations
for combo in combinations(cards_5, 4):
y += count_divisible_by_11(combo)
x, y
問6
1,2,3,4,5,6,7,8から異なる4つを選び,大きい方から順にA,B,C,Dとしました。また,選ばなかった残りの4つを並び替え,E,F,G,Hとしました。すると,4桁の数ABCDから4桁の数DCBAを引いた差は4桁の数EFGHでした。4桁の数ABCDを求めよ。
回答
これは正解ですね。
この問題を解くためには、与えられた数字から異なる4つを選び、大きい方から小さい方に向かってA, B, C, Dと命名し、残った4つをE, F, G, Hとして、その数が等しくなるようにする必要があります。この問題を解決するために、すべての可能性を試すことが一つの方法です。
まず、数字1から8までの中から異なる4つの数字を選び、その数字を大きい順にA, B, C, Dとし、4桁の数ABCDとDCBAを作成して、その差が他の4つの数字で表される4桁の数EFGHに一致するかどうかを調べます。この作業を自動化するためにプログラムを使用します。
計算結果から、選ばれた4桁の数 ABCD として 8532 があります。この数から逆順に配置した数 DCBA を引いた差 6174 は、選ばれなかった4つの数字を並び替えて得られる4桁の数 EFGH として 6174 に一致します。したがって、求める4桁の数 ABCD は 8532 です。
from itertools import permutations, combinations
# Generate all possible combinations of choosing 4 digits out of [1, 2, 3, 4, 5, 6, 7, 8]
all_combinations = combinations([1, 2, 3, 4, 5, 6, 7, 8], 4)
# Function to calculate the number from digits
def digits_to_number(digits):
return int("".join(map(str, digits)))
# Function to find the remaining digits
def remaining_digits(full_set, selected_set):
return tuple(d for d in full_set if d not in selected_set)
# Dictionary to hold possible solutions
possible_solutions = []
# Set of all digits
full_set = {1, 2, 3, 4, 5, 6, 7, 8}
# Check each combination
for combination in all_combinations:
sorted_combination = tuple(sorted(combination, reverse=True)) # Sort to get ABCD
remaining = remaining_digits(full_set, sorted_combination)
ABCD = digits_to_number(sorted_combination)
DCBA = digits_to_number(sorted_combination[::-1])
diff = ABCD - DCBA
# Now check all permutations of the remaining digits to see if any form the difference
for perm in permutations(remaining):
EFGH = digits_to_number(perm)
if EFGH == diff:
possible_solutions.append((ABCD, EFGH))
possible_solutions
問7から問12
ここからは図形問題ですが、回答がさっぱりなので軽く触れます。
特に問9については、円の半径がどこかが認識できていません。幾何学的な図形の認識はできないと考えた方がいいですね。